Polygons Edges/Vertices

Name of polygon Number of edges and vertices
Triangle 3 edges and vertices
Quadrilateral 4 edges and vertices
Pentagon 5 edges and vertices
Hexagon 6 edges and vertices
Heptagon 7 edges and vertices
Octogon 8 edges and vertices
Nonagon 9 edges and vertices
Decagon 10 edges and vertices
Hendecagon/Undecagon 11 edges and vertices
Dodecagon 12 edges and vertices
Tridecagon 13 edges and vertices
Tetradecagon/Tetrakaidecagon 14 edges and vertices
Pentadecagon/Pentakaidecagon 15 edges and vertices
Hexadecagon/Hexakaidecagon 16 edges and vertices
Heptadecagon 17 edges and vertices
Octadecagon/Octakaidecagon 18 edges and vertices
Enneadecagon/Enneakaidecagon 19 edges and vertices
Icosagon 20 edges and vertices

Sum of all Internal Angles in a Polygon

Sum of all Angles = (n-2)*180

n=number of sides

Shape Sum of Angles
Triangle 180
Quadrilateral 360
Pentagon 540
Hexagon 720
Heptagon 900
Octagon 1080
Nonagon 1260
Decagon 1440
Undecagon 1620
Dodecagon 1800
Tridecagon 1980
Tetradecagon 2160
Pentadecagon 2340
Hexadecagon 2520
Heptadecagon 2700
Octadecagon 2880
Enneadecagon 3060
Icosagon 3240

Polygon Area for most Common Shapes

b=base

l= length

w=width

h=height

a=side

b1=base #1

d1=diagonal #1 

sqrt()= square root of number in parenthesis

Shape Formula
Triangles b*h/2
Rectangle/square l*w
Rhombus d1*d2/2
Trapezoid (b1+b2)*h

Area of a Hexagon Equation- 

Area of a Pentagon Equation and Explanation-

http://jwilson.coe.uga.edu/EMAT6680/Parsons/MVP6690/Unit/Pentagon/pentagon.html

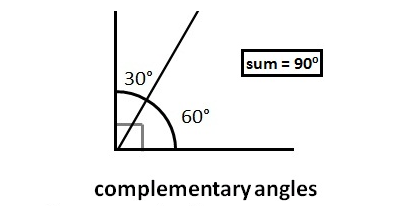
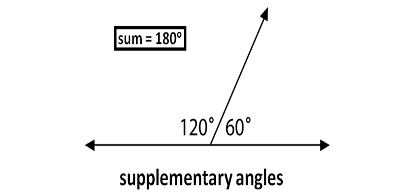
Complementary and Supplementary Angles

A complementary angle is made when the given angle is subtracted by 90 degrees.

A supplementary angle is made when the given angle is subtracted by 180 degrees. 

x=given value

Complementary formula=90-x

Supplementary formula=180-x